초보 개발자의 일기
최단 경로 (다익스트라 알고리즘) 본문
최단경로 알고리즘
최단경로 알고리즘: 가장 짧은 경로를 찾는 알고리즘

노드: 각 지점은 그래프에서 노드로 표현
간선: 지점 간 연결된 도로는 그래프에서 간선으로 표현
최단 경로 알고리즘은 대표적으로 다익스트라 최단 경로 알고리즘, 플로이드 워셜, 벨만 포드 알고리즘 이렇게 3개이다.
이 중에서 다익스트라 최단 경로 알고리즘, 플로이드 워셜을 공부해보자.
다익스트라 최단 경로 알고리즘
그래프에서 여러 개의 노드가 있을 때, 특정한 노드에서 출발하여 다른 노드로 가는 각각의 최단 경로를 구해주는 알고리즘
음의 간선이 없을 때 정상적으로 작동
알고리즘의 원리
- 출발 노드를 설정
- 최단 거리 테이블을 초기화
- 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택
- 해당 노드를 거쳐 다른 노드로 가는 비용을 계산해 최단 거리 테이블 갱신
- 위 과정에서 3번 4번을 반복
작동 예시

출발 노드를 1번으로 선택
초기 상태에서는 다른 모든 노드로 가는 최단거리를 무한(inf)으로 설정

출발 노드를 1번으로 선택하고 거리를 0으로 설정
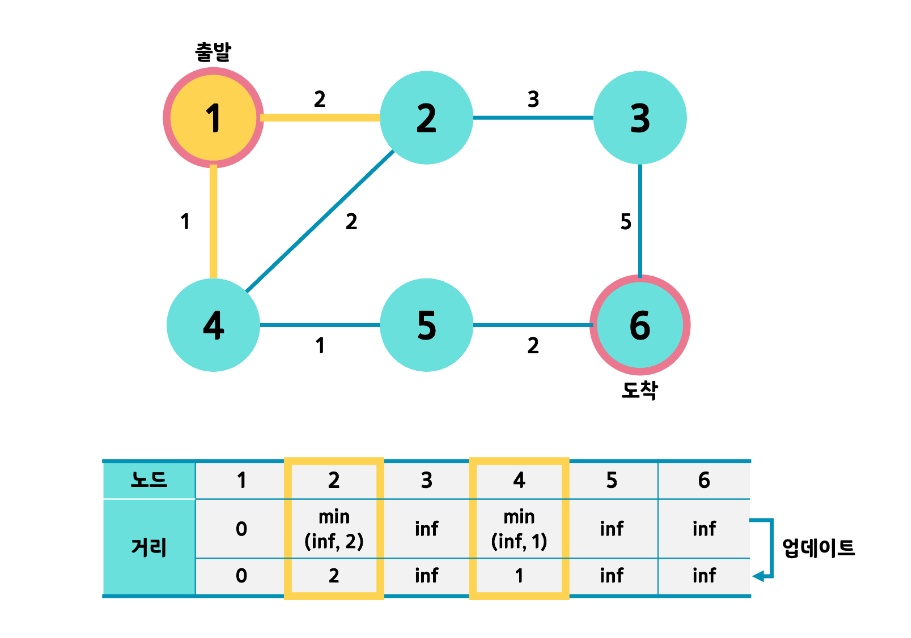
1번 노드를 거쳐 다른 노드로 가는 비용을 계산한다.
갈 수 없는 다른 노드들은 그대로 inf로 둔다.
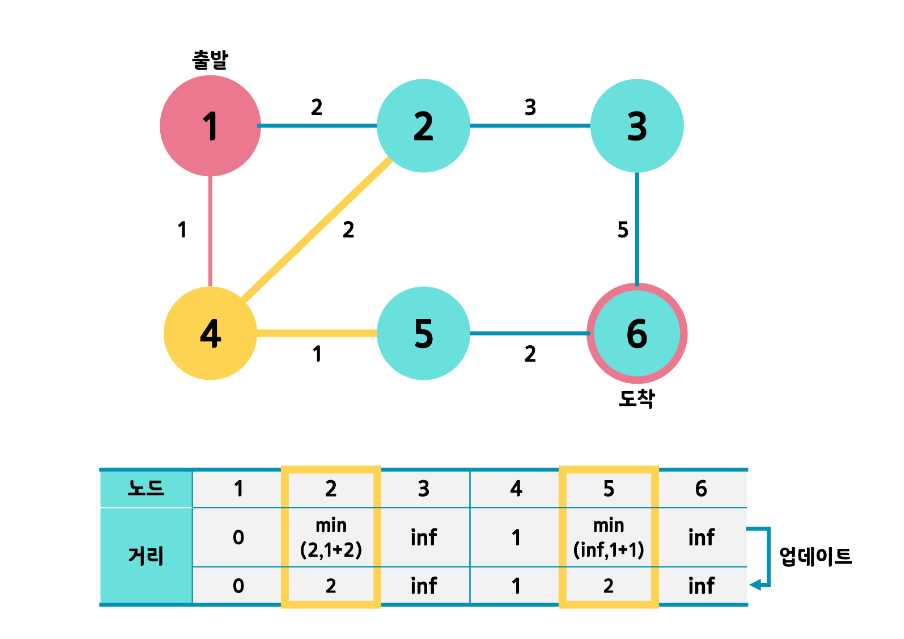
이제 방문하지 않는 노드들 중 최단 거리가 가장 짧은 노드를 선택해야 한다.
위 그림에서는 최단 거리가 1인 4번 노드가 선택되었다.
이제 4번 노드에서 다른 노드로 갈 수 있는 최단 경로를 모두 업데이트한다.
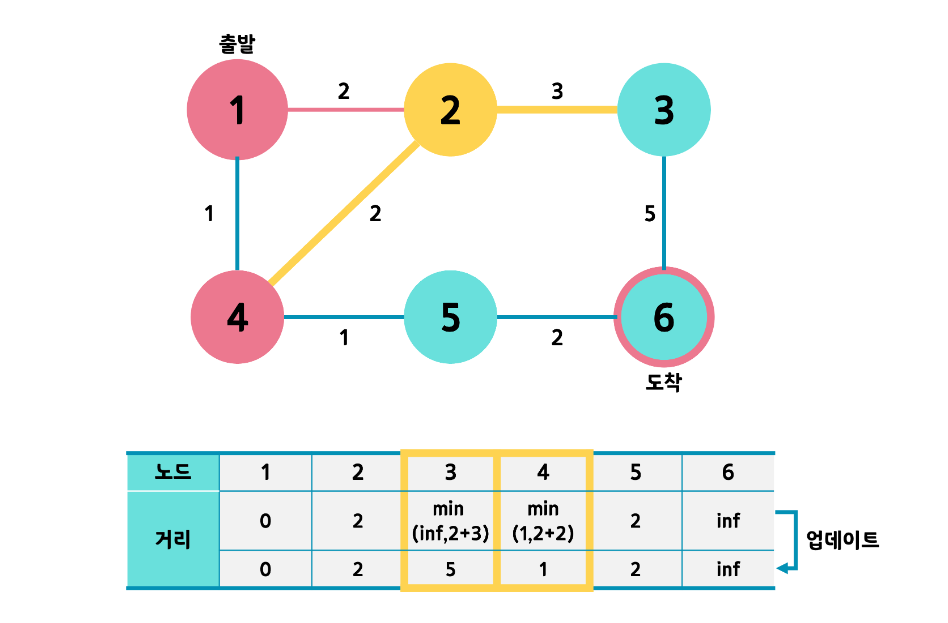
최단 경로가 2로 2번 노드와 5번 노드가 동률인데 이럴 때는 인덱스의 크기가 작은 것을 우선으로 선택해 2번 노드를
선택하고 2번 노드를 통해 최단 경로를 모두 업데이트한다.
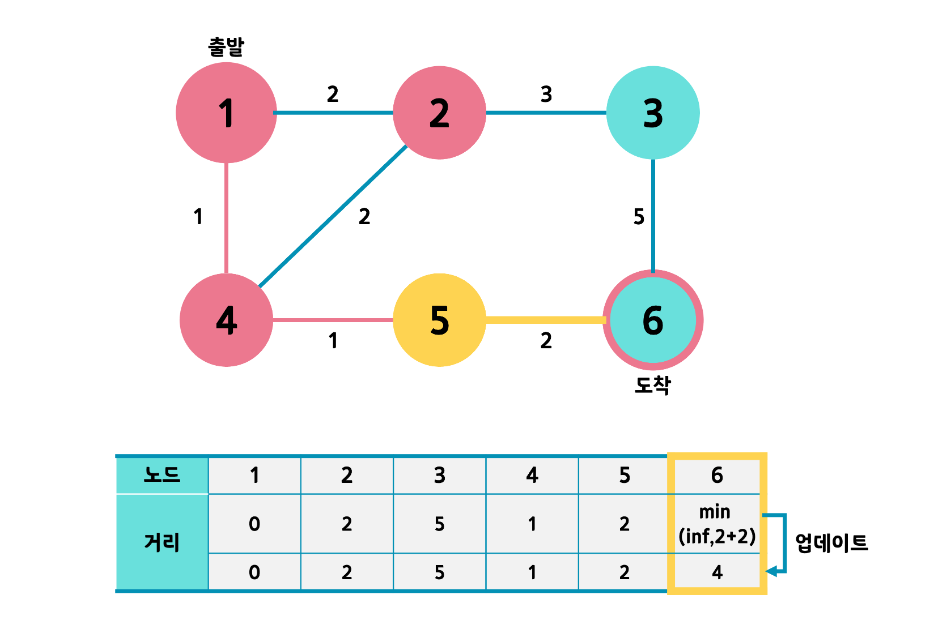
아직 방문하지 않은 노드들 중 최단경로가 2인 5번 노드를 선택하고 5번 노드를 통해 갈 수 있는 경로를
모두 업데이트한다.
이후 모든 과정을 반복하여 결과 값을 찾는다.
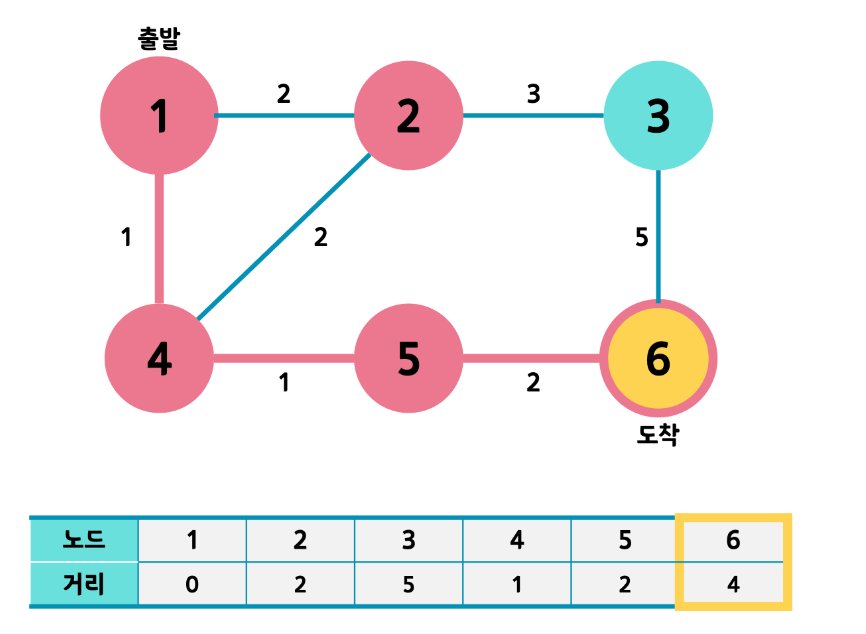
마지막으로 도착하는 노드는 6번 노드이며 6번 노드까지 오는 경로는
1- 4 - 5 - 6의 경로를 거쳐 최소 거리는 4가 된다.
이렇게 다익스트라 알고리즘이 진행되면서 한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는 것으로 이해할 수 있다.
간단한 다익스트라 알고리즘
처음에 각 노드에 대한 최단 거리를 담는 1차원 리스트를 선언한다.
이후 단계마다 방문하지 않는 노드 중에서 최단 거리가 가장 짧은 노드를 선택하기 위해 매 단계마다 1차원 리스트의 모든 원소를 확인한다.
시간 복잡도는 O(V^2)이다.
V는 노드의 개수를 의미한다.
최단 경로 문제에서 전체 노드의 개수가 5000개 이하라면 이 코드로 문제를 풀 수 있지만,
노드의 개수가 10000개가 넘으면 이 코드로는 문제를 해결하기 어렵다.
간단한 다익스트라 알고리즘 코드
import sys
input = sys.stdin.readline
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정
# 노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
# 시작 노드 번호를 입력받기
start = int(input())
# 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for i in range(n + 1)]
# 방문한 적이 있는지 체크하는 목적의 리스트를 만들기
visited = [False] * (n + 1)
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n + 1)
# 모든 간선 정보를 입력받기
for _ in range(m):
a, b, c = map(int, input().split())
# a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].append((b, c))
# 방문하지 않은 노드 중에서, 가장 최단 거리가 짧은 노드의 번호를 반환
def get_smallest_node():
min_value = INF
index = 0 # 가장 최단 거리가 짧은 노드(인덱스)
for i in range(1, n + 1):
if distance[i] < min_value and not visited[i]:
min_value = distance[i]
index = i
return index
def dijkstra(start):
# 시작 노드에 대해서 초기화
distance[start] = 0
visited[start] = True
for j in graph[start]:
distance[j[0]] = j[1]
# 시작 노드를 제외한 전체 n - 1개의 노드에 대해 반복
for i in range(n - 1):
# 현재 최단 거리가 가장 짧은 노드를 꺼내서, 방문 처리
now = get_smallest_node()
visited[now] = True
# 현재 노드와 연결된 다른 노드를 확인
for j in graph[now]:
cost = distance[now] + j[1]
# 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[j[0]]:
distance[j[0]] = cost
# 다익스트라 알고리즘을 수행
dijkstra(start)
# 모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n + 1):
# 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if distance[i] == INF:
print("INFINITY")
# 도달할 수 있는 경우 거리를 출력
else:
print(distance[i])개선된 다익스트라 알고리즘
간단한 다익스트라 알고리즘은 최단 거리가 가장 짧은 노드를 찾기 위해, 매번 최단 거리 테이블을 선형적(모든 원소를 앞에서부터 하나씩)으로 탐색해야 했다.
개선된 다익스 트랑 알고리즘에서는 Heap 자료구조를 사용한다.
개선된 다익스트라 알고리즘 코드
import heapq
import sys
input = sys.stdin.readline
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정
# 노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
# 시작 노드 번호를 입력받기
start = int(input())
# 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for i in range(n + 1)]
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n + 1)
# 모든 간선 정보를 입력받기
for _ in range(m):
a, b, c = map(int, input().split())
# a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].append((b, c))
def dijkstra(start):
q = []
# 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
heapq.heappush(q, (0, start))
distance[start] = 0
while q: # 큐가 비어있지 않다면
# 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
dist, now = heapq.heappop(q)
# 현재 노드가 이미 처리된 적이 있는 노드라면 무시
if distance[now] < dist:
continue
# 현재 노드와 연결된 다른 인접한 노드들을 확인
for i in graph[now]:
cost = dist + i[1]
# 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0]))
# 다익스트라 알고리즘을 수행
dijkstra(start)
# 모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n + 1):
# 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if distance[i] == INF:
print("INFINITY")
# 도달할 수 있는 경우 거리를 출력
else:
print(distance[i])'코딩테스트 > 이것이 코딩테스트다.(Python)' 카테고리의 다른 글
| 플로이드 워셜 알고리즘 (0) | 2022.07.31 |
|---|---|
| 효율적인 화폐 구성 (1) | 2022.07.22 |
| 바닥 공사 (0) | 2022.07.21 |
| 개미 전사 (2) | 2022.07.12 |
| 1로 만들기 (1) | 2022.07.10 |




